基于频次与极值外推综合的载荷外推总体方法

doi:10.12382/bgxb.2023.0072

摘要/Abstract

摘要：

载荷外推作为载荷谱编制的重要技术手段,当前研究缺乏对于载荷外推总体方法的全面梳理、马尔可夫稳态分布的求解方法适应性不够、缺乏不同非参频次外推方法的比较与选用原则,导致不便生成高精度载荷谱以支撑装备性能设计。围绕坦克在高机动和极限工况下的载荷谱编制问题,基于某坦克行进间身管位移数据样本,分别使用基于雨流矩阵及核密度估计的非参数外推法、基于马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)的信号重构法以及Metropolis-Hastings(简称MH)直接采样法进行了载荷频次外推,并针对MCMC的信号重构法提出了一种改良马尔可夫稳态分布的求解方法。应用所提出的频次-极值相结合的载荷外推总体方法对坦克身管位移进行了频次扩充与极值预测,并结合实车试验结果验证了方法的准确性。研究结果表明:改良的马尔可夫稳态分布求解方法是有效的;在样本长度足够、外推精度要求不甚高的情况下,MH直接采样法可作为一种新的频次外推方法;运用频次-极值相结合的载荷外推总体方法所得结果精度较高;形成的频次外推法选用原则对于载荷谱编制过程中的方法选择具有一定的指导意义。研究工作为装备载荷谱的高质量编制提供了成熟的技术路线和参考。

关键词: 载荷外推, 核密度估计, 马尔可夫链蒙特卡洛方法, 马尔可夫稳态分布, Metropolis-Hastings采样

Abstract:

Load extrapolation, as an important technical means for compiling load spectra, is inconvenient to generate the high-precision load spectra to support equipment performance design due to lacking of the comprehensive review of overall load extrapolation method, the insufficient adaptability of solution method for Markov steady-state distribution, and the comparison and selection principles for different nonparametric frequency extrapolation methods. Focusing on the compilation of tank’s load spectrum under high mobility and extreme conditions, the nonparametric extrapolation method based on rain flow matrix and kernel density estimation, the signal reconstruction based on Markov Chain Monte Carlo (MCMC) method, and the Metropolis-Hastings (MH) direct sampling method are used to perform the frequency extrapolation according to the barrel displacement dataset of a tank in motion. Besides, an improved Markov steady-state distribution solution method is proposed for the signal reconstruction method of MCMC. Finally, the proposed overall frequency-extreme load extrapolation method is used to expand the frequency and predict the extreme values of the dataset. The accuracy of overall method is verified based on experimental results. It is shown that the improved Markov steady-state distribution solution method is effective. The MH direct sampling method can be used as a new frequency extrapolation method when the sample length is sufficient and the extrapolation accuracy is not very high. The accuracy of overall frequency-extreme load extrapolation method is relatively high. The principles for selecting frequency extrapolation methods have certain guiding significance for the selection of methods in the process of compiling the load spectra. The research work provides a mature technical route and reference for the high-quality equipment load spectra compiling.

Key words: load extrapolation, kernel density estimation, Markov Chain Monte Carlo method, Markov steady-state distribution, Metropolis-Hastings sampling

中图分类号:

TJ303

高华, 单春来, 刘军, 张凡凡, 刘朋科. 基于频次与极值外推综合的载荷外推总体方法[J]. 兵工学报, 2024, 45(6): 1942-1953.

GAO Hua, SHAN Chunlai, LIU Jun, ZHANG Fanfan, LIU Pengke. Overall Load Extrapolation Method Based on Frequency and Extreme Value Extrapolation[J]. Acta Armamentarii, 2024, 45(6): 1942-1953.

图/表 22

图1 载荷外推总体方法

Fig.1 Overall load extrapolation method

图2 MH采样法原理图解

Fig.2 Schematic diagram of MH sampling method

图3 二维MH采样代码

Fig.3 The code of 2D MH sampling

图4 基于MCMC的信号重构操作流程

Fig.4 Operation process of signal reconstruction based on MCMC

图5 某坦克身管位移-时间预处理后结果(C级路,25km/h)

Fig.5 Displacement-time graph of a tank barrel after pretreatment (Level C road, 25km/h)

图6 身管位移From-To矩阵(C级路面,25km/h)

Fig.6 Barrel displacement From-To matrix (Level C road, 25km/h)

图7 身管位移From-To矩阵(三维)

Fig.7 Barrel displacement From-To matrix (3D)

图8 雨流矩阵核密度估计结果

Fig.8 Kernel density estimation results of rain flow matrix

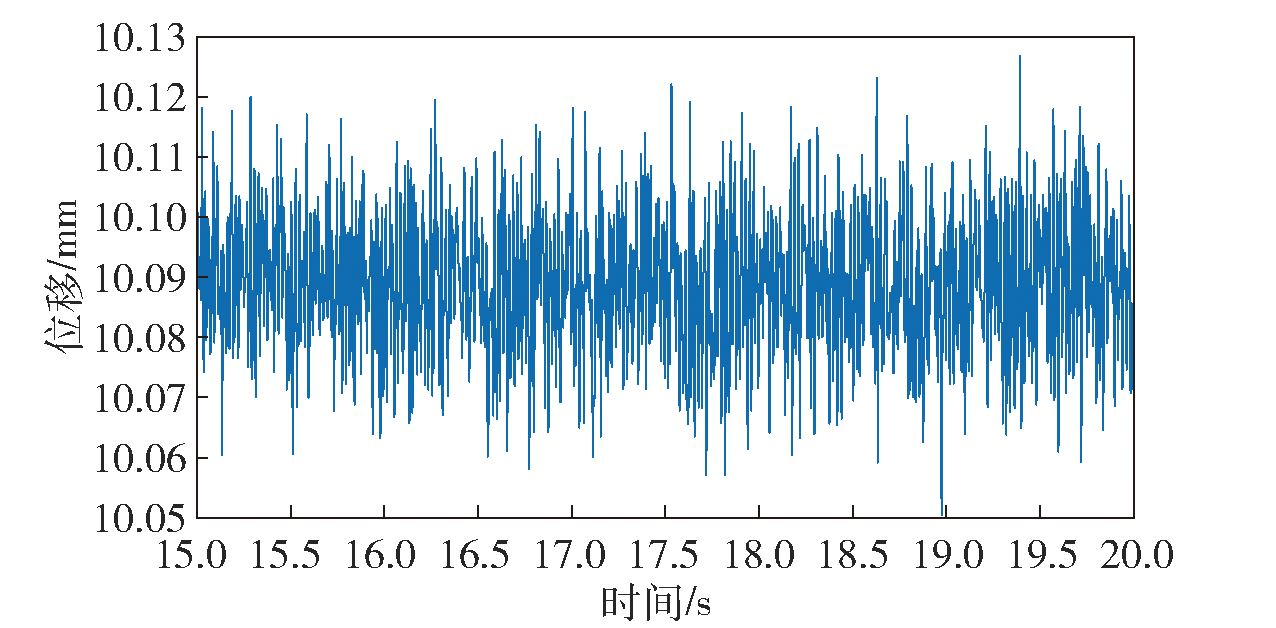
图9 基于雨流矩阵及核密度估计的非参数频次外推时序信号(局部)

Fig.9 Nonparametric frequency extrapolation of time-series signals based on rain flow matrix and kernel density estimation (partial)

图10 基于MCMC的信号重构后时序信号

Fig.10 Time-series signal based on the signal reconstruction method of MCMC

图11 MH直接采样后时序信号(局部)

Fig.11 Time-series signal after MH direct sampling (partial)

表1 3种频次外推前后统计对比

Table 1 Statistical comparison before and after frequency extrapolation by 3 methodsmm

类别	均值	标准差	前20个极大值			前20个极小值
类别	均值	标准差	最大值	均值	中位数	最小值	均值	中位数
外推前	10.0884	0.0111	10.1288	10.1227	10.1214	10.0533	10.0574	10.0574
方法1	10.0888	0.0111	10.1267	10.1202	10.1193	10.0504	10.0585	10.0594
方法2	10.0884	0.011	10.1277	10.1268	10.1277	10.0546	10.055	10.0546
方法3	10.0886	0.011	10.1285	10.126	10.126	10.0495	10.055	10.0555

图12 3种频次外推前后概率密度对比

Fig.12 Comparison of probability densities before and after frequency extrapolation by 3 methods

图13 不同数据量下外推前后概率密度(方法3)

Fig.13 Probability densities before and after extrapolation under different data volumes (Method 3)

表2 不同数据量下外推前后概率密度差值统计(方法3)

Table 2 Probability density difference statistics before and after extrapolation under different data volumes (Method 3)

n	最大值	均值	标准差
1000	3.0768	-0.1356	2.3830
3000	1.6686	0.2764	2.1118
5000	-0.81	0.1148	1.2565

图14 3种频次外推前后功率谱对比

Fig.14 Comparison of power spectra before and after frequency extrapolation by 3 methods

表3 3种外推方法关键因素及优缺点比较

Table 3 Comparison of key factors and advantage/disadvantage of three extrapolation methods

外推方法	关键因素	优点	缺点
方法1	核函数的选择,最优带宽确定	与样本的分布类型无关,任意形状载荷谱的有效估计	需要大量样本数据,核函数和带宽选择是有影响的
方法2	马尔可夫分布初始状态,状态转移矩阵	基本不需要调参,可兼顾载荷与时间间隔^[7]	需要判断是否马氏收敛,求解马尔可夫初始状态繁琐
方法3	最小样本长度	操作简单、外推方便	样本长度需要校验

图15 频次外推后信号的MEF曲线

Fig.15 MEF curve of signal after frequency extrapolation

图16 超阈值经验分布与理论分布对比

Fig.16 Comparison between empirical distribution and theoretical distribution of over threshold value

图17 极值外推后的位移时间信号

Fig.17 Displacement-time signal after extremum extrapolation

图18 验证试验时序信号

Fig.18 Time-series signals of verification test

图19 验证试验与载荷外推概率密度对比

Fig.19 Probability density comparison of verification test and load extrapolation

参考文献 21

[1]	PARZEN E. On estimation of a probability density function and mode[J]. Annals of Mathematical Statistics, 1962, 33(3): 1065-1076.
[2]	SILVERMAN B W. Density estimation for statistics and data analysis[M]. NY, US: Routledge, 2018.
[3]	张建成. 基于核函数的数控车床载荷谱编制关键技术研究[D]. 长春: 吉林大学, 2019.
	ZHANG J C. Research on key technologies for compiling load spectrum of CNC lathe based on kernel function[D]. Changchun: Jilin University, 2019. (in Chinese)
[4]	刘海鸥, 张文胜, 徐宜, 等. 基于核密度估计的履带车辆传动轴载荷谱编制[J]. 兵工学报, 2017, 38(9): 1830-1838. doi: 10.3969/j.issn.1000-1093.2017.09.021
	LIU H O, ZHANG W S, XU Y, et al. Load spectrum compiling for transmission shaft of tracked vehicle based on kernel density estimation[J]. Acta Armamentarii, 2017, 38(9):1830-1838. (in Chinese)
[5]	高天宇, 李焕良, 郑铮, 等. 基于雨流频次外推的ZLK50型装载机液压缸载荷谱编制[J]. 机械强度, 2017, 39(4): 951-956.
	GAO T Y, LI H L, ZHENG Z, et al. Compiling method of load spectrum of ZLK50 type loader hydraulic cylinder based on rain flow frequency extrapolation[J]. Journal of Mechanical Strength, 2017, 39(4):951-956. (in Chinese)
[6]	WANG J X, ZHANG J H, LIANG Y L, et al. A cyclic simulation approach for the generation of the non-stationary load histories of engineering vehicles[J]. Journal of Mechanical Science & Technology, 2012, 26(5):1547-1554.
[7]	YANG Z H, SONG Z H, ZHAO X Y, et al. Time-domain extrapolation method for tractor drive shaft loads in stationary operating conditions[J]. Biosystems Engineering, 2021, 210:143-155.
[8]	武玉倩. 基于隐马尔可夫模型的装载机载荷谱编制方法研究[D]. 长春: 吉林大学, 2017.
	WU Y Q. Research on load spectra compilation method of loaders based on hidden Markov model[D]. Changchun: Jilin University, 2017. (in Chinese)
[9]	SCARROTT C, MACDONALD A. A review of extreme value threshold estimation and uncertainty quantification authors:[J]. Revstat-Statistical Journal, 2012, 10(1):33-60.
[10]	JOHANNESSON P. Extrapolation of load histories and spectra[J]. Fatigue & Fracture of Engineering Materials & Structures, 2006, 29(3):201-207.
[11]	江柱锦. 混合动力装载机电机载荷外推方法研究[D]. 长春: 吉林大学, 2018.
	JIANG Z J. Research on load extrapolation method of hybrid loader motor[D]. Changchun: Jilin University, 2018. (in Chinese)
[12]	翟新婷. 基于外推改进的工程机械载荷谱编制方法研究[D]. 长春: 吉林大学, 2018.
	ZHAI X T. Load spectrum compiling method based on modified extrapolation in construction machinery[D]. Changchun: Jilin University, 2018. (in Chinese)
[13]	何佳龙. 数控车床切削力谱的编制及其在功能部件可靠性试验中的应用[D]. 长春: 吉林大学, 2017.
	HE J L. Arial compilation of cutting force spectrum of CNC lathe and its application in reliability test[D]. Changchun: Jilin University, 2017. (in Chinese)
[14]	CAO R, CUEVAS A, GONZALEZ M W. A comparative study of several smoothing methods in density estimation[J]. Computational Statistics & Data Analysis, 1994, 17(2):153-176.
[15]	高飞, 潘长明, 孙磊. Bayes匹配场地声参数反演:多步退火Gibbs采样算法[J]. 兵工学报, 2017, 38(7): 1385-1394. doi: 10.3969/j.issn.1000-1093.2017.07.017
	GAO F, PAN C M, SUN L. Geoacoustic parameters inversion of Bayes matched-field: a multi-annealing Gibbs sampling algorithm[J]. Acta Armamentarii, 2017, 38(7): 1385-1394. (in Chinese) doi: 10.3969/j.issn.1000-1093.2017.07.017
[16]	WANG J X, CHEN H B, LI Y, et al. A review of the extrapolation method in load spectrum compiling[J]. Strojniski Vestnik-journal of Mechanical Engineering, 2016, 62(1):60-75.
[17]	ZHENG G F, WANG Q Y, CAI C. Criterion to determine the minimum sample size for load spectrum measurement and statistical extrapolation[J]. Measurement, 2021, 178:109387.
[18]	李斌潮, 唐靖, 殷之平. 基于频率雨流计数法的发动机振动疲劳载荷谱编制[J]. 航空工程进展, 2021, 12(1): 24-29.
	LI B C, TANG J, YIN Z P. The load spectrum compilation of engine vibration fatigue based on frequency rain-flow counting method[J]. Advances in Aeronautical Science and Engineering, 2021, 12(1):24-29. (in Chinese)
[19]	BASBUG B B, WYNN H P. Patterns in the Turkish reinsurance claim data, 1998—2002: an application of the extreme value theory[J]. Natural Hazards, 2006, 39(2):329-342.
[20]	WANG H J, XUAN F Z, LIU X T. Prediction and evaluation of fatigue life under random load based on low load strengthening characteristic[J]. International Journal of Fatigue, 2021, 151:106346.
[21]	HE J L, ZHAO X Y, LI G F, et al. Time domain load extrapolation method for CNC machine tools based on GRA-POT model[J]. The International Journal of Advanced Manufacturing Technology, 2019, 103(7):3799-3812.