基于塑性弦线法的深水爆炸下加筋锥柱壳变形模型

doi:10.12382/bgxb.2022.0726

摘要/Abstract

摘要：

为探究凸型加筋锥柱壳在静水压与深水爆炸载荷联合作用下的动态响应,在塑性弦线模型基础上考虑静水压载荷、锥角因素,将问题简化为求解拥有初边界值的波动方程,利用特征值展开将肋间板壳径向位移表示为无穷级数的形式,并对每个特征值计算相应的卸载时间,以此显示冲击波载荷的衰减特性。使用有限元程序Abaqus对半锥角为20°的凸型加筋锥柱壳开展最大深度500m、最大冲击因子0.79kg^0.5/m的水下爆炸数值模拟研究,对邻近结合处的柱段、锥段肋间板壳的理论模型计算结果进行验证对比和讨论。研究结果表明:与不计静水压相比,静水压使得肋间板壳刚度减小——最大位移出现时刻延滞,最终径向位移随水深而增大;在不同冲击因子下,理论模型与数值模拟最终径向位移误差最大为21.7%(锥段),最小为2.0%(柱段);由于锥角的存在,肋间板壳位移不再关于中心点对称分布,中心点最终位移较柱段减小40%以上。

关键词: 加筋锥柱壳, 塑性弦线, 深水爆炸, 特征值卸载

Abstract:

In order to explore the dynamic response of a convex reinforced conical-cylindrical shell under the combined action of hydrostatic pressure and deep-underwater explosion load, the hydrostatic pressure load and cone angle factors are added on the plastic string model, and the problem is simplified to resolve the wave equation with initial value and boundary conditions. The radial displacement of the intercostal shell is expressed as an infinite series by using the expansion of eigenvalue, and the corresponding unloading time is calculated for each eigenvalue, so as to show the attenuation characteristics of shock wave load. The finite element program Abaqus is used to carry out a numerical simulation study of underwater explosion with a maximum depth of 500m and a maximum impact factor of 0.79kg^0.5/m for a convex stiffened cylindrical shell with a half-cone angle of 20°. The results of theoretical model calculation of cylindrical and cone intercostal shells adjacent to the joint are verified, compared and discussed. The results show that, compared with that without hydrostatic pressure, the hydrostatic pressure decreases the stiffness of intercostal shells, which delays the maximum displacement, and the final radial displacement increases with water depth. Under different impact factors, the ultimate radial displacement error between the theoretical model and the numerical simulation is 21.7% (cone section) and 2.0% (column section), respectively. At the same time, due to the presence of cone angle, the shell displacements are no longer symmetrically distributed about the center point, and the final displacement of the center point is reduced by more than 40% compared with the column segment.

Key words: ring-stiffened conical-cylinderical shell, plastic string, deep-underwater explosion, unloading of eigenvalue

中图分类号:

O383

汪海洋, 龙仁荣, 张庆明, 刘博文, 廖晨. 基于塑性弦线法的深水爆炸下加筋锥柱壳变形模型[J]. 兵工学报, 2024, 45(3): 705-719.

WANG Haiyang, LONG Renrong, ZHANG Qingming, LIU Bowen, LIAO Chen. Deformation Model of Ring-stiffened Conical-cylindrical Shell under Deep-underwater Explosion Based on Plastic String Method[J]. Acta Armamentarii, 2024, 45(3): 705-719.

图/表 27

图1 深水爆炸载荷曲线

Fig.1 Loading curve of underwater explosion

图2 凸型加筋锥柱壳示意图

Fig.2 Schematic diagram of convex reinforced cone-cylinder combined shell

图3 横截面壳变形机制[6]

Fig.3 Deformation mechanism of cross-section shell[6]

图4 塑性弦线模型

Fig.4 Plastic string model

图5 环筋力平衡方程

Fig.5 Force balance equation of ring stiffener

表1 波动方程参数

Table 1 Wave equation parameters

参数	意义
$x ˜$ = $x l$	轴向坐标
$t ˜$ = $t c l / c o s α$	时间
$w ˜$ =w· $N ¯ (l / c o s α) 2 q ¯$	肋间板壳瞬时径向位移
γ= $l / c o s α c θ d$	波传播时间与爆炸载荷持续时间比
ζ= $Q ¯ q ¯ l / c o s α$	T型筋与弦线刚度比
η= $M ¯ m ¯ l / c o s α$	T型筋与弦线质量比
$p ˜$ = $p ¯ q ¯$	载荷与抗力比

表1 波动方程参数

Table 1 Wave equation parameters

参数	意义
$x ˜$ = $x l$	轴向坐标
$t ˜$ = $t c l / c o s α$	时间
$w ˜$ =w· $N ¯ (l / c o s α) 2 q ¯$	肋间板壳瞬时径向位移
γ= $l / c o s α c θ d$	波传播时间与爆炸载荷持续时间比
ζ= $Q ¯ q ¯ l / c o s α$	T型筋与弦线刚度比
η= $M ¯ m ¯ l / c o s α$	T型筋与弦线质量比
$p ˜$ = $p ¯ q ¯$	载荷与抗力比

图6 实验与仿真模型对比

Fig.6 Comparison of experimental and simulation models

表2 Q345的J-C模型参数

Table 2 Parameters of J-C model of Q345

ρ/ (kg·m^-3)	E/ GPa	μ	A/ MPa	B/ MPa	n	C	ν
7850	210	0.28	375	630	0.52	0.032	1.03

图7 实验和数值模拟变形特征对比

Fig.7 Comparison between experimental and simulated deformation features

表3 实验和数值仿真结果对比汇总

Table 3 Comparison between experimental and simulated results

变形	实验结果	仿真结果	误差/%
结合处向外隆起变形/mm	4	3.55	-11.3
柱段靠近结合处一跨向内凹陷变形/mm	6	5.02	-16.3

表4 柱段板壳波动方程参数

Table 4 Parameters of wave equation of cylinder section

参数	数值
$x ˜$ = $x l$	0
$t ˜$ = $t c l$
$w ˜$ =w· $N ¯ l 2 q ¯$
γ= $l c θ d$	2.70
ζ= $Q ¯ q ¯ l$	18.06
η= $M ¯ m ¯ l$	3.16
$p ¯$ = $p ¯ q ¯$	184.17

表4 柱段板壳波动方程参数

Table 4 Parameters of wave equation of cylinder section

参数	数值
$x ˜$ = $x l$	0
$t ˜$ = $t c l$
$w ˜$ =w· $N ¯ l 2 q ¯$
γ= $l c θ d$	2.70
ζ= $Q ¯ q ¯ l$	18.06
η= $M ¯ m ¯ l$	3.16
$p ¯$ = $p ¯ q ¯$	184.17

表5 柱段板壳波动方程特征值

Table 5 Eigenvalues of wave equation in cylinder section

序列	数值	序列	数值
λ₀	0	λ₁₀	29.86
λ₁	1.89	λ₁₁	33.00
λ₂	4.84	λ₁₂	36.14
λ₃	7.93	λ₁₃	39.28
λ₄	11.05	λ₁₄	42.42
λ₅	14.18	λ₁₅	45.56
λ₆	17.31	λ₁₆	48.70
λ₇	20.45	λ₁₇	51.84
λ₈	23.58	λ₁₈	54.98
λ₉	26.72	λ₁₉	58.13

表6 特征值对应卸载时间(柱)

Table 6 The unloading time corresponding to the eigenvalue (cylinder)

序列	数值	序列	数值
$t ˜ 0$	66.30	$t ˜ 10$	0.081
$t ˜ 1$	0.87	$t ˜ 11$	0.075
$t ˜ 2$	0.48	$t ˜ 12$	0.070
$t ˜ 3$	0.21	$t ˜ 13$	0.065
$t ˜ 4$	0.16	$t ˜ 14$	0.061
$t ˜ 5$	0.14	$t ˜ 15$	0.058
$t ˜ 6$	0.12	$t ˜ 16$	0.055
$t ˜ 7$	0.11	$t ˜ 17$	0.052
$t ˜ 8$	0.097	$t ˜ 18$	0.049
$t ˜ 9$	0.088	$t ˜ 19$	0.047

表6 特征值对应卸载时间(柱)

Table 6 The unloading time corresponding to the eigenvalue (cylinder)

序列	数值	序列	数值
$t ˜ 0$	66.30	$t ˜ 10$	0.081
$t ˜ 1$	0.87	$t ˜ 11$	0.075
$t ˜ 2$	0.48	$t ˜ 12$	0.070
$t ˜ 3$	0.21	$t ˜ 13$	0.065
$t ˜ 4$	0.16	$t ˜ 14$	0.061
$t ˜ 5$	0.14	$t ˜ 15$	0.058
$t ˜ 6$	0.12	$t ˜ 16$	0.055
$t ˜ 7$	0.11	$t ˜ 17$	0.052
$t ˜ 8$	0.097	$t ˜ 18$	0.049
$t ˜ 9$	0.088	$t ˜ 19$	0.047

图8 柱段板壳中心点瞬时径向位移对比

Fig.8 Comparison of transient radial displacements of center point of cylindrical shell

图9 不计静水压柱段板壳中心点瞬时径向位移对比

Fig.9 Comparison of transient radial displacements of center point of cylindrical shell without hydrostatic pressure

图10 不同水深柱段板壳中心点瞬时径向位移对比

Fig.10 Comparison of transient radial displacements of center point of cylindrical shell under different water depths

图11 不同水深柱段板壳中心点最终位移对比

Fig.11 Comparison of final displacements of center point of cylindrical shell under different water depths

图12 柱段板壳最终径向位移波形对比

Fig.12 Waveform comparison of final radial displacement of cylindrical shell

图13 不同冲击因子柱段板壳中心点最终位移对比

Fig.13 Comparison of final displacements of shell center point of cylinder section with different SF

表7 锥段板壳波动方程参数

Table 7 Parameters of wave equation of cone section

参数	数值
$x ˜$ = $x l$	0
$t ˜$ = $t c l / c o s α$
$w ˜$ =w· $N ¯ (l / c o s α) 2 q ¯$
γ= $l / c o s α c θ d$	2.87
ζ= $Q ¯ q ¯ l / c o s α$	18.06
η= $M ¯ m ¯ l / c o s α$	2.97
$p ˜$ = $p ¯ q ¯$	156.73

表7 锥段板壳波动方程参数

Table 7 Parameters of wave equation of cone section

参数	数值
$x ˜$ = $x l$	0
$t ˜$ = $t c l / c o s α$
$w ˜$ =w· $N ¯ (l / c o s α) 2 q ¯$
γ= $l / c o s α c θ d$	2.87
ζ= $Q ¯ q ¯ l / c o s α$	18.06
η= $M ¯ m ¯ l / c o s α$	2.97
$p ˜$ = $p ¯ q ¯$	156.73

表8 锥段板壳波动方程特征值

Table 8 Eigenvalues of wave equation of cone section

序列	数值	序列	数值
λ₀	0	λ₁₀	29.86
λ₁	1.97	λ₁₁	33.00
λ₂	4.85	λ₁₂	36.14
λ₃	7.94	λ₁₃	39.29
λ₄	11.06	λ₁₄	42.43
λ₅	14.18	λ₁₅	45.57
λ₆	17.32	λ₁₆	48.71
λ₇	20.45	λ₁₇	51.85
λ₈	23.59	λ₁₈	54.99
λ₉	26.73	λ₁₉	58.13

表9 特征值对应卸载时间(锥)

Table 9 The unloading time corresponding to the eigenvalue (cone)

序列	数值	序列	数值
$t ˜ 0$	63.22	$t ˜ 10$	0.081
$t ˜ 1$	0.87	$t ˜ 11$	0.075
$t ˜ 2$	0.32	$t ˜ 12$	0.070
$t ˜ 3$	0.20	$t ˜ 13$	0.065
$t ˜ 4$	0.16	$t ˜ 14$	0.061
$t ˜ 5$	0.14	$t ˜ 15$	0.058
$t ˜ 6$	0.12	$t ˜ 16$	0.055
$t ˜ 7$	0.11	$t ˜ 17$	0.052
$t ˜ 8$	0.10	$t ˜ 18$	0.050
$t ˜ 9$	0.088	$t ˜ 19$	0.047

表9 特征值对应卸载时间(锥)

Table 9 The unloading time corresponding to the eigenvalue (cone)

序列	数值	序列	数值
$t ˜ 0$	63.22	$t ˜ 10$	0.081
$t ˜ 1$	0.87	$t ˜ 11$	0.075
$t ˜ 2$	0.32	$t ˜ 12$	0.070
$t ˜ 3$	0.20	$t ˜ 13$	0.065
$t ˜ 4$	0.16	$t ˜ 14$	0.061
$t ˜ 5$	0.14	$t ˜ 15$	0.058
$t ˜ 6$	0.12	$t ˜ 16$	0.055
$t ˜ 7$	0.11	$t ˜ 17$	0.052
$t ˜ 8$	0.10	$t ˜ 18$	0.050
$t ˜ 9$	0.088	$t ˜ 19$	0.047

图14 锥段板壳中心点瞬时径向位移对比

Fig.14 Comparison of transient radial displacements of center point of conical shell

图15 不同冲击环境锥段板壳中心点最终位移对比

Fig.15 Comparison of final displacements of center point of conical shell under different impact environment

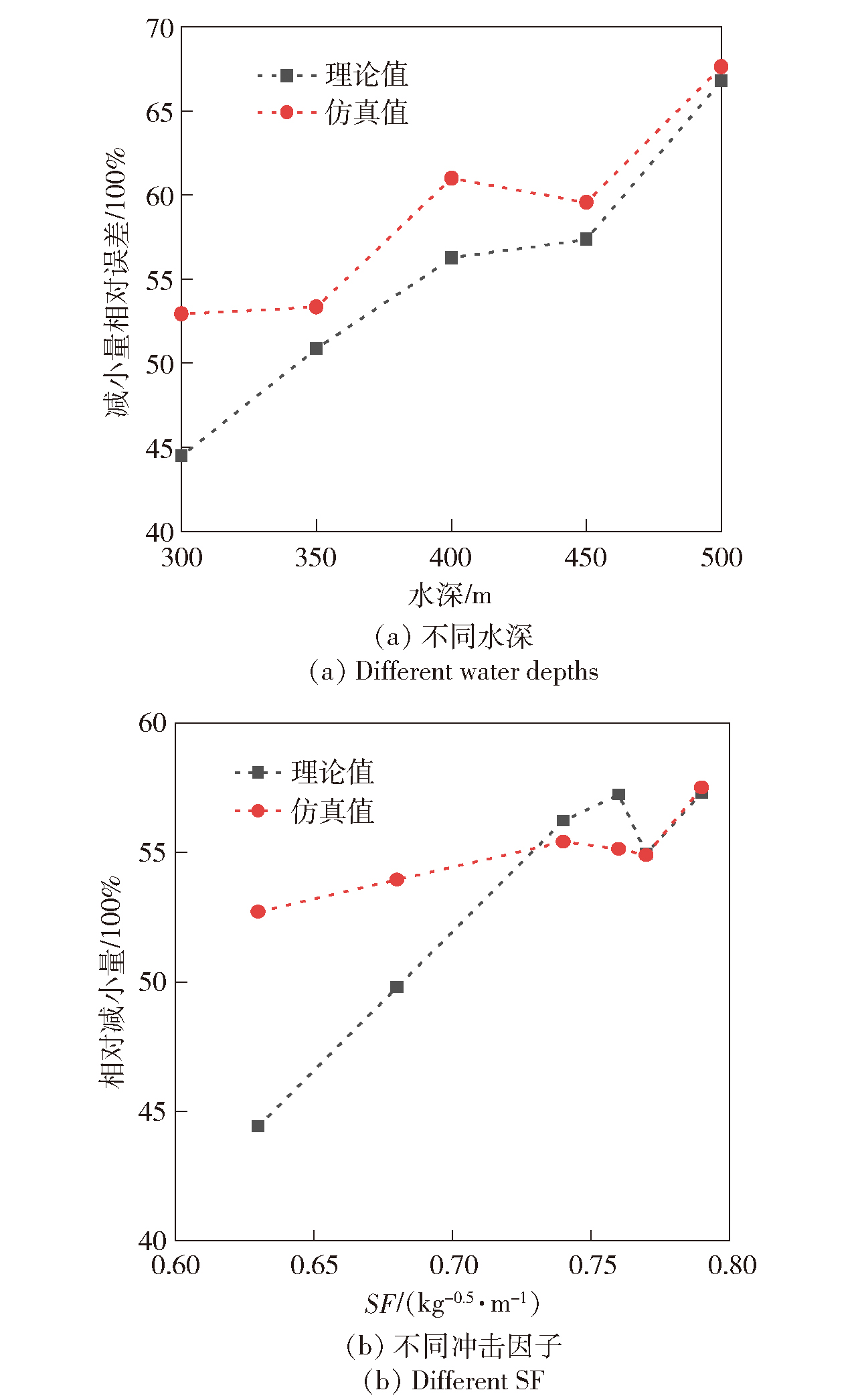
图16 不同冲击环境下锥段板壳中心点最终位移较柱段减小量

Fig.16 The reduction of the final displacements of the center point of the conical plate shell compared with that of the column under different impact environments

图17 锥段板壳最终径向位移波形对比

Fig.17 Waveform comparison of final radial displacement of conical shell

图18 不同冲击因子下锥段板壳最终径向位移波形

Fig.18 The final radial displacement waveforms of conical shell under different SF

参考文献 22

[1]	HODGE P G. Impact pressure loading of rigid-plastic cylindrical shells[J/OL]. Journal of the Mechanics and Physics of Solids, 1955, 3(3): 176-188.
[2]	徐秉业. 结构塑性极限分析[M]. 北京: 中国建筑工业出版社, 1985.
	XU B Y. Structural plastic limit analysis[M]. Beijing: China Construction Industry Press, 1985. (in Chinese)
[3]	GEFKEN P R, KIRKPATRICK S W, HOLMES B S. Response of impulsively loaded cylindrical shells[J]. International Journal of Impact Engineering, 1988, 7(2):213-227. doi: 10.1016/0734-743X(88)90027-9 URL
[4]	WIERZBICKI T, HOO F M S. Impact response of a string-on-plastic foundation[J]. International Journal of Impact Engineering, 1992, 12(1):21-36. doi: 10.1016/0734-743X(92)90304-C URL
[5]	WIERZBICKI T, HOO F M S. Damage assessment of cylinders due to impact and explosive loading[J]. International Journal of Impact Engineering, 1993, 13(2):215-241. doi: 10.1016/0734-743X(93)90094-N URL
[6]	HOO F M S. Deformation and rupture of cylindrical shells under dynamic loading thesis[D]. Cambridge, MA, US: MIT, 1992.
[7]	BROCHARD K, LE SOURNE H, BARRAS G. Extension of the string-on-foundation method to study the shock wave response of an immersed cylinder[J]. International Journal of Impact Engineering, 2018, 117: 138-152. doi: 10.1016/j.ijimpeng.2018.03.007 URL
[8]	LI J, HUA H X. Transient response of an orthotropic cylindrical shell to an underwater explosive loading[J]. Journal of Reinforced Plastics and Composites, 2009, 28(14): 1747-1762. doi: 10.1177/0731684408090374 URL
[9]	SUN W F, ZHU T T, CHEN P W, et al. Dynamic implosion of submerged cylindrical shell under the combined hydrostatic and shock loading[J]. Thin-Walled Structures, 2022, 170: 108574. doi: 10.1016/j.tws.2021.108574 URL
[10]	BROCHARD K, SOURNE H L, BARRAS G. A simplified method to assess the damage of an immersed cylinder subjected to underwater explosion[M]// Progress in the Analysis and Design of Marine Structures. Boca Raton, FL, US: CRC Press, 2017.
[11]	BROCHARD K, LE SOURNE H, BARRAS G. Estimation of the response of a deeply immersed cylinder to the shock wave generated by an underwater explosion[J]. Marine Structures, 2020, 72:102786. doi: 10.1016/j.marstruc.2020.102786 URL
[12]	BRETT J M, YIANNAKOPOLOUS G. A study of explosive effects in close proximity to a submerged cylinder[J]. International Journal of Impact Engineering, 2008, 35(4):206-225. doi: 10.1016/j.ijimpeng.2007.01.007 URL
[13]	卢熹, 王树山, 马峰, 等. 水下爆炸环肋圆筒损伤特性实验及数值模拟[J]. 北京理工大学学报, 2015, 35(10):995-1000.
	LU X, WANG S S, MA F, et al. Experimental and numerical study of damage characteristics for ring-stiffened cylinder subjected to underwater explosion[J]. Transactions of Beijing Institute of Technology, 2015, 35(10): 995-1000. (in Chinese)
[14]	YUAN J H, ZHU X. Dynamic response of a ring-stiffened cylindrical shell subjected to underwater explosive loading[J]. Applied Mechanics and Materials, 2012, 105-107:931-936. doi: 10.4028/www.scientific.net/AMM.105-107 URL
[15]	NAGAI T. On the results of damages of cylindrical shells due to underwater explosion[J]. Journal of Zosen Kiokai, 1996, 1966(119):108-115. doi: 10.2534/jjasnaoe1952.1966.108 URL
[16]	梁浩哲, 张庆明, 龙仁荣, 等. 凸型加筋錐柱壳结构深水爆炸下的破坏模式[J]. 兵工学报, 2021, 42(5):987-996.
	LIANG H Z, ZHANG Q M, LONG R R, et al. Failure modes of ring-stiffened convex cone-cylinder at deep underwater explosion[J]. Acta Armamentarii, 2021, 42(5):987-996. (in Chinese)
[17]	余晓菲, 刘土光, 张涛, 等. 水下爆炸载荷作用下加筋圆柱壳的响应分析[J]. 振动与冲击, 2006, 26(5): 106-115,195-196.
	YU X F, LIU T G, ZHANG T, et al. Response analysis of stiffened cylindrical shell under underwater explosion shock waves[J]. Journal of Vibration and Shock, 2006, 26(5):106-115,195-196. (in Chinese)
[18]	贾宪振, 胡毅亭, 董明荣, 等. 深水环境中水下爆炸冲击波作用下圆柱壳动态响应的数值模拟研究[J]. 振动与冲击, 2008, 28(5):160-165,182.
	JIA X Z, HU Y T, DONG M R, et al. Dynamic response of cylindrical shell subjected to underwater explosion shock waves in deep water[J]. Journal of Vibration and Shock, 2008, 28(5): 160-165,182. (in Chinese)
[19]	姚熊亮, 王玉红, 史冬岩, 等. 圆筒结构水下爆炸数值实验研究[J]. 哈尔滨工程大学学报, 2002, 23(1): 5-8,36.
	YAO X L, WANG Y H, SHI D Y, et al. Numerical experiment on underwater explosion of cylinder[J]. Journal of Harbin Engineering University, 2002, 23(1):5-8,36. (in Chinese)
[20]	杨一方. 水下爆炸冲击载荷等效加载方法研究[D]. 南京: 南京理工大学, 2015.
	YANG Y F. Research on equivalent loading method of underwater explosion shock load[D]. Nanjing: Nanjing University of Science and Technology, 2015. (in Chinese)
[21]	ZHU X, ZHANG Z H, FENG G, et al. Experimental and numerical investigations of the dynamic response of ring-stiffened cylinder subjected to underwater explosion[J]. Journal of Beijing Institute of Technology 2004(3):346-350.
[22]	贺平, 严勇. 圆筒水下爆炸冲击响应[J]. 数字海洋与水下攻防, 2021, 4(5):405-411.
	HE P, YAN Y. Shock response of cylindrical shell to underwater explosion[J]. Digital Ocean & Underwater Warfare, 2021, 4(5):405-411. (in Chinese)